Difference between revisions of "Scoring"

From zFairs Contest Management
(Created)
Line 15: Line 15:
  
 
== z-Score ==
 
== z-Score ==
−
: This is a normalized score that takes into account all of the scores assigned by a given judge for a single round, normalizes them and returns a score based on the deviation from the standard for the score applied to the project.
+
: This is a normalized score that takes into account all of the scores assigned by a given judge for a single round. It does this by taking each raw score it then normalizes them and returns a score based on the average and the standard deviation.
  
 
:{|
 
:{|
Line 24: Line 24:
 
: What that translates to for zFairs is:
 
: What that translates to for zFairs is:
 
:: In a given round a judge assigns scores to projects. Those scores are evaluated and an Avg & SD (Standard Deviation) value are calculated. Those values are plugged in to the formula as seen above and each raw score from that judge is then normalized to a value representing how different from their standard score it is. Values that are negative are below the average score for the judge and values that are positive are above the judge's average score.
 
:: In a given round a judge assigns scores to projects. Those scores are evaluated and an Avg & SD (Standard Deviation) value are calculated. Those values are plugged in to the formula as seen above and each raw score from that judge is then normalized to a value representing how different from their standard score it is. Values that are negative are below the average score for the judge and values that are positive are above the judge's average score.
−
:: The end result and take away is that the z-score adjusts for the fact that some judges score higher in general whereas others score lower for the same effort and quality of project. Teams and Projects are then less affected by luck of the draw in regards to the judges they have assigned to judge them.
+
:: The end result is that the z-score adjusts for the fact that some judges score higher in general whereas others score lower for the same effort and quality of project. Teams and Projects are then less affected by luck of the draw in regards to the judges they have assigned to judge them.
  
 
: An Example of this would be:
 
: An Example of this would be:
Line 30: Line 30:
 
:: Judge B judges the same 7 projects and assigns the following scores out of 100: 61, 59, 63, 70, 67, 54 and 67
 
:: Judge B judges the same 7 projects and assigns the following scores out of 100: 61, 59, 63, 70, 67, 54 and 67
 
:: Judge C judges the same 7 projects and assigns the following scores out of 100: 44, 37, 45, 42, 39, 41 and 45
 
:: Judge C judges the same 7 projects and assigns the following scores out of 100: 44, 37, 45, 42, 39, 41 and 45
−
:: The mean / average for Judge A is 83.43 <small>(rounded up to two decimal places for convenience)</small>
+
:: The mean / average for Judge A is 83.43
−
:: The mean / average for Judge B is 63 <small>(this was not rounded nor was it planned but it is convenient)</small>
+
:: The mean / average for Judge B is 63
−
:: The mean / average for Judge C is 41.86 <small>(rounded up to two decimal places for convenience)</small>
+
:: The mean / average for Judge C is 41.86
 
:: So for Judge A, B and C we calculate the z-scores as follows:
 
:: So for Judge A, B and C we calculate the z-scores as follows:
−
:::{|
+
::{| class="wikitable" style="text-align:center;"
 +
|-
 +
|  || Avg=83.43<br/> SD=1.38 || Avg=63<br/> SD=1.23 || Avg=41.86<br/> SD=0.96
 
|-
 
|-
 
! Project !! Judge A !! Judge B !! Judge C
 
! Project !! Judge A !! Judge B !! Judge C
−
|-
 
−
! || Avg=83.43 & SD=1.38 || Avg=63 & SD=1.23 || Avg=41.86 & SD=0.96
 
 
|-
 
|-
 
|
 
|
Line 49: Line 49:
 
#
 
#
 
|
 
|
−
(87-83.43)/1.38 = +2.59
+
+2.59 <br/>
−
(74-83.43)/1.38 = -6.83
+
-6.83 <br/>
−
(91-83.43)/1.38 = +5.49
+
+5.49 <br/>
−
(83-83.43)/1.38 = -0.31
+
-0.31 <br/>
−
(77-83.43)/1.38 = -4.66
+
-4.66 <br/>
−
(82-83.43)/1.38 = -1.04
+
-1.04 <br/>
−
(90-83.43)/1.38 = +4.76
+
+4.76
 
|
 
|
−
(61-63)/1.23 = -1.63
+
-1.63 <br/>
−
(59-63)/1.23 = -3.25
+
-3.25 <br/>
−
(63-63)/1.23 = 0.00
+
0.00 <br/>
−
(70-63)/1.23 = +5.69
+
+5.69 <br/>
−
(67-63)/1.23 = +3.25
+
+3.25 <br/>
−
(54-63)/1.23 = -7.32
+
-7.32 <br/>
−
(67-63)/1.23 = +3.25
+
+3.25
 
|  
 
|  
−
(44-41.86)/0.96 = +2.23
+
+2.23 <br/>
−
(37-41.86)/0.96 = -5.06
+
-5.06 <br/>
−
(45-41.86)/0.96 = +3.27
+
+3.27 <br/>
−
(42-41.86)/0.96 = +0.15
+
+0.15 <br/>
−
(39-41.86)/0.96 = -2.98
+
-2.98 <br/>
−
(41-41.86)/0.96 = -0.90
+
-0.90 <br/>
−
(45-41.86)/0.96 = +3.27
+
+3.27
 
|}
 
|}
 
|}
 
|}
Line 77: Line 77:
  
 
: Some helpful articles for reading on better understanding z-score values:
 
: Some helpful articles for reading on better understanding z-score values:
−
:* [https://en.wikipedia.org/wiki/Standard_score]
+
:* https://en.wikipedia.org/wiki/Standard_score
−
:* [https://www.statisticshowto.com/probability-and-statistics/z-score/]
+
:* https://www.statisticshowto.com/probability-and-statistics/z-score/
−
:* [https://www.simplypsychology.org/z-score.html]
+
:* https://www.simplypsychology.org/z-score.html
 +
 
 +
 
 +
 
 +
<br/><br/><br/><br/>
 +
[[Category: Staff]]
 +
[[Category: Admin]]
 +
[[Category: Judging]]

Revision as of 16:07, 6 January 2021

Scoring each project takes much consideration and deliberation by each judge. Unfortunately making sense of that score afterwards and determining the best Project Scores can also take much consideration and deliberation. On this page we cover that in a little more detail so you have the information needed to make the best decisions possible.
For each Project and Judging result you will have access to up to 4 different scores. These are the Average Score for the Project, the Adjusted Score, the Raw Score and the Z-Score. See below for clarification on each of the individual scoring types.

Average Score

This score takes the average out of all scores for a given project and presents that as its value.


Adjusted Score

This score... (Please update me)


Raw Score

This is the score as given by the judge(s) without any calculations or normalizations being applied.

z-Score

This is a normalized score that takes into account all of the scores assigned by a given judge for a single round. It does this by taking each raw score it then normalizes them and returns a score based on the average and the standard deviation.

Formula

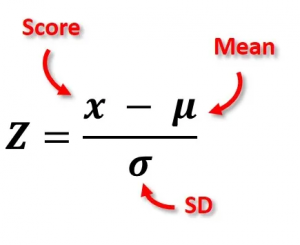
Z-Score Formula

z-score is equal to the raw score minus the population mean, divided by the population standard deviation.
What that translates to for zFairs is:
In a given round a judge assigns scores to projects. Those scores are evaluated and an Avg & SD (Standard Deviation) value are calculated. Those values are plugged in to the formula as seen above and each raw score from that judge is then normalized to a value representing how different from their standard score it is. Values that are negative are below the average score for the judge and values that are positive are above the judge's average score.
The end result is that the z-score adjusts for the fact that some judges score higher in general whereas others score lower for the same effort and quality of project. Teams and Projects are then less affected by luck of the draw in regards to the judges they have assigned to judge them.
An Example of this would be:
Judge A judges 7 different projects and assigns the following scores out of 100: 87, 74, 91, 83, 77, 82 and 90
Judge B judges the same 7 projects and assigns the following scores out of 100: 61, 59, 63, 70, 67, 54 and 67
Judge C judges the same 7 projects and assigns the following scores out of 100: 44, 37, 45, 42, 39, 41 and 45
The mean / average for Judge A is 83.43
The mean / average for Judge B is 63
The mean / average for Judge C is 41.86
So for Judge A, B and C we calculate the z-scores as follows:
Avg=83.43
SD=1.38		 Avg=63
SD=1.23		 Avg=41.86
SD=0.96
Project Judge A Judge B Judge C

+2.59
-6.83
+5.49
-0.31
-4.66
-1.04
+4.76

-1.63
-3.25
0.00
+5.69
+3.25
-7.32
+3.25

+2.23
-5.06
+3.27
+0.15
-2.98
-0.90
+3.27


Some helpful articles for reading on better understanding z-score values:






Retrieved from "https://wiki.zfairs.com/index.php?title=Scoring&oldid=280"